728x90
step 2 - 4. 정수 삼각형
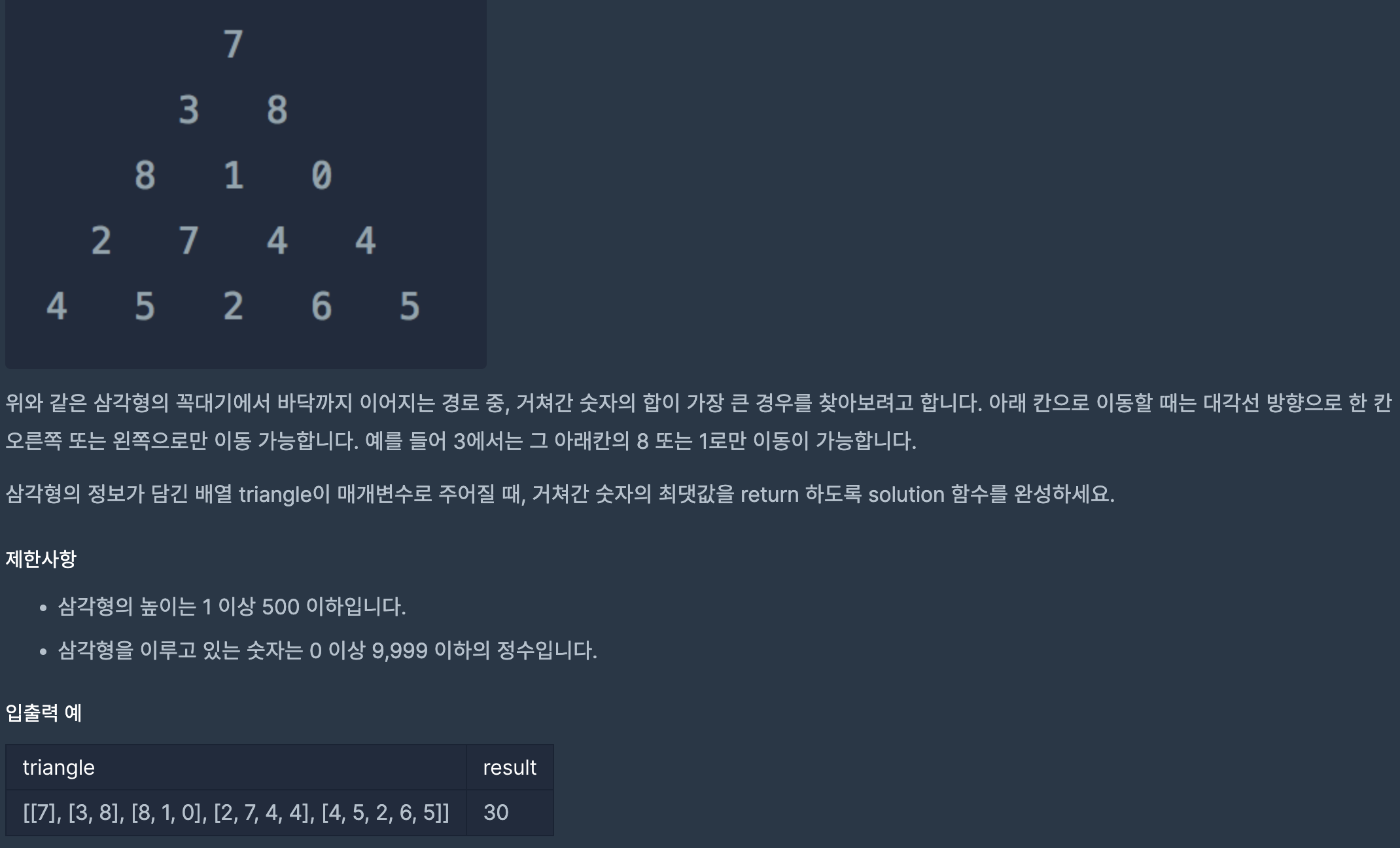
내가 떠올린 풀이 해설
- DP 삼각형의 가장 왼쪽의 값 (DP[i][0])은 한 줄 위의 가장 왼쪽 값(DP[i - 1][0])에 현재 값(triangle[i][0])을 더한 값이 된다.
DP[i][0] = DP[i-1][0] + triangle[i][0]이 됩니다. - 삼각형의 가장 오른쪽의 값 (DP[i][i])은 한 줄 위의 가장 오른쪽 값(DP[i-1][i-1])에 현재 값(triangle[i][i])을 더한 값이 된다.
DP[i][i] = DP[i-1][i-1] + triangle[i][i]이 됩니다. - 삼각형의 1번과 2번을 제외한 나머지는 한줄 위의 오른쪽 값과 왼쪽 값 중 큰 값에 현재 값을 더한 값이 된다.
DP[i][i] = Max(DP[i - 1][j - 1], DP[i - 1][j]) + triangle[i][j]가 됩니다. - DP 배열에서 max 값을 출력하기 위해 answer = Math.max(answer, dp[i][j])을 해준다.
정확한 풀이
public class step2_4 {
public static void main(String[] args) {
int[][] tri = {{7},
{3, 8},
{8, 1, 0},
{2, 7, 4, 4},
{4, 5, 2, 6, 5}};
int [][]dp = new int[tri.length][tri[tri.length - 1].length];
int answer = 0;
int max = 0;
dp[0][0] = tri[0][0];
for(int i = 1; i < tri.length; i++) {
dp[i][0] = dp[i - 1][0] + tri[i][0];
dp[i][i] = dp[i - 1][i - 1] + tri[i][i];
for(int j = 1; j <= i - 1; j++) {
dp[i][j] = Math.max(dp[i - 1][j - 1], dp[i - 1][j]) + tri[i][j];
answer = Math.max(answer, dp[i][j]);
}
}
System.out.println(answer);
}
}
오늘의 회고
오늘은 DP문제와 프로그래머스 위장 문제와 유사한 문제를 백준에서 찾아서 HashMap 문제를 풀었습니다. 점화식은 도출을 해냈지만 DP 배열을 만들 생각을 하지 못하고 triangle 배열에서 점화식을 처리해주려고 했는데 생각처럼 되지 않았습니다. HashMap문제는 거의 동일해서 어렵지 않게 해결할 수 있었습니다. 알고리즘 고수가 되고 싶습니다.ㅠㅠ
728x90
'알고리즘 > 프로그래머스 커뮤러닝' 카테고리의 다른 글
| [커뮤러닝/6기] 3주차 step 2 - 3. 올바른 괄호의 개수 (0) | 2022.07.22 |
|---|---|
| [커뮤러닝/6기] 3주차 step 2 - 2. 게임 맵 최단거리 (0) | 2022.07.21 |
| [커뮤러닝/6기] 3주차 step 2 - 1. 위장 (0) | 2022.07.20 |
| [커뮤러닝/6기] 1주차 step 1 - 4. 숫자 게임 (0) | 2022.07.10 |
| [커뮤러닝/6기] 1주차 step [1 - 2 ~ 1 - 3] 가장 큰 수, 예산 (0) | 2022.07.07 |