69번 문자열 집합

내가 떠올린 풀이 해설
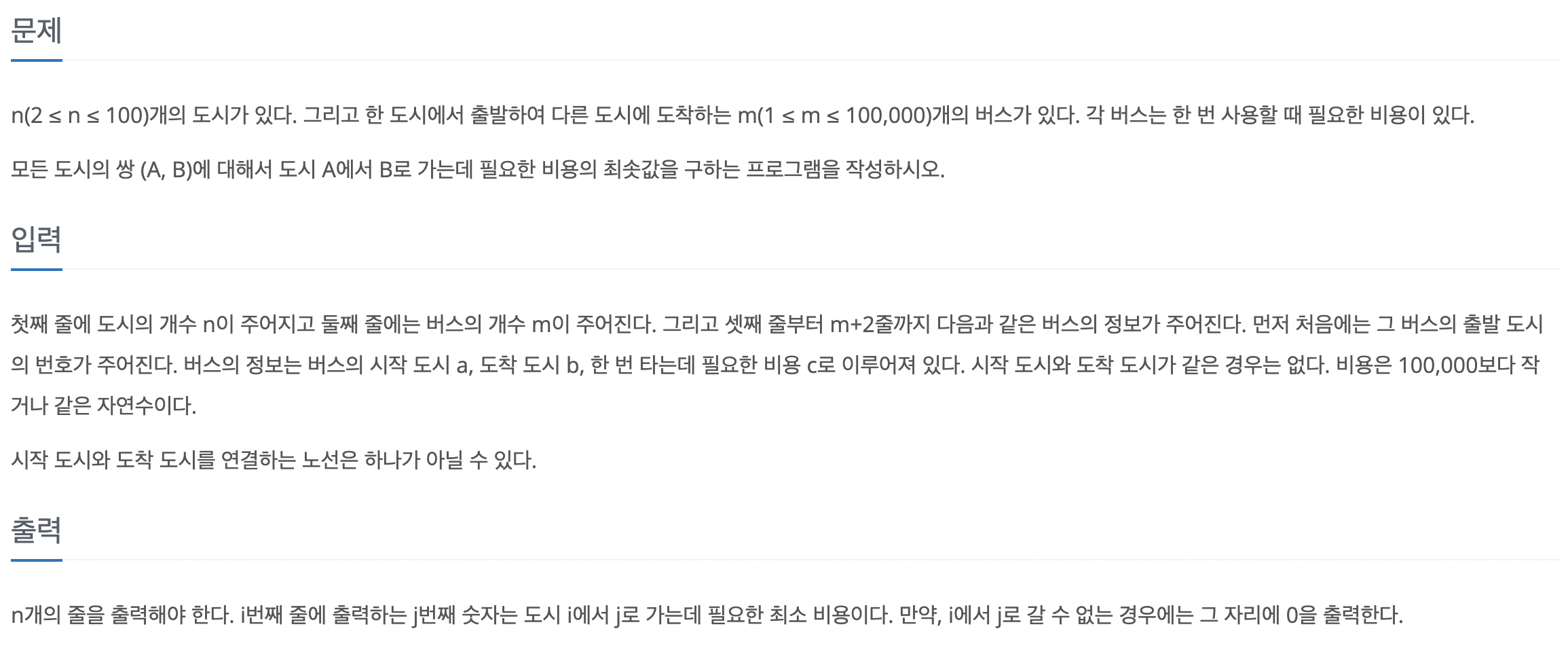
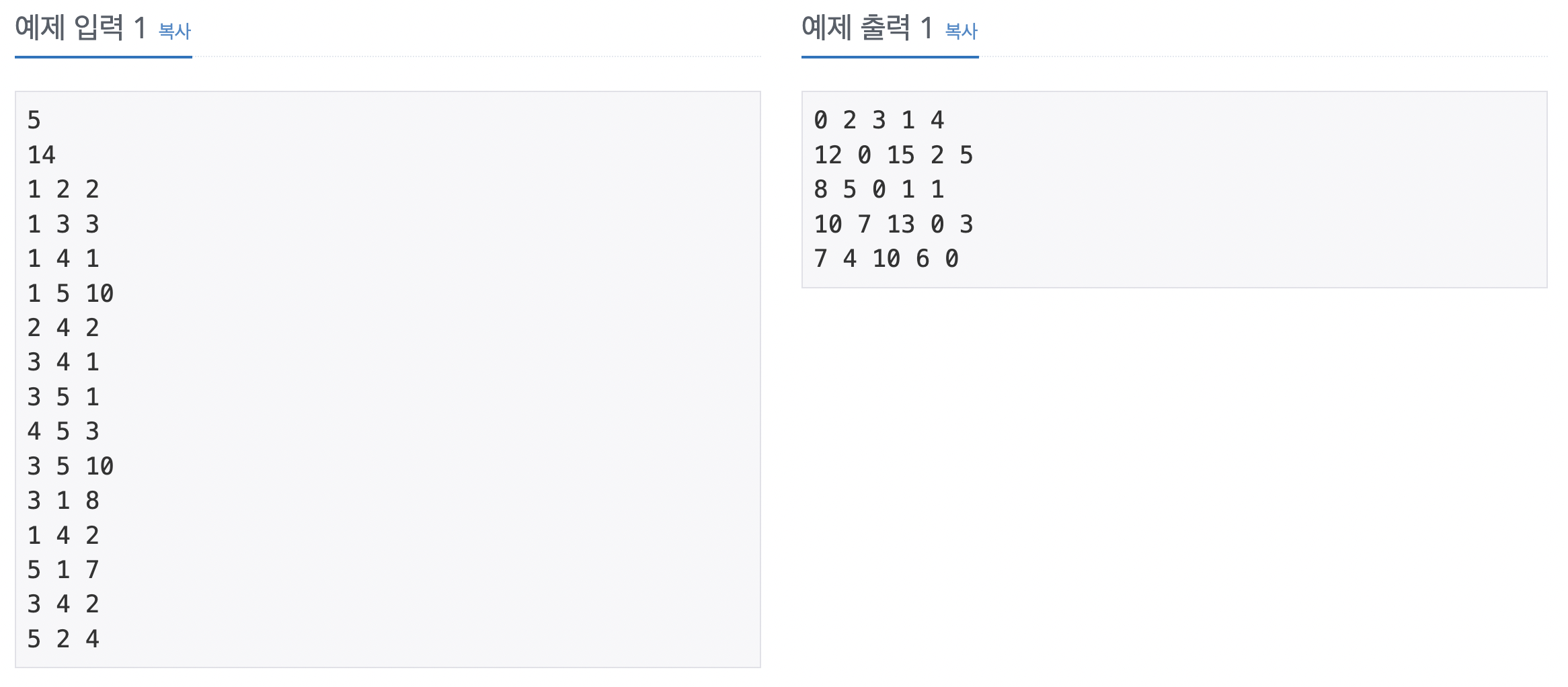
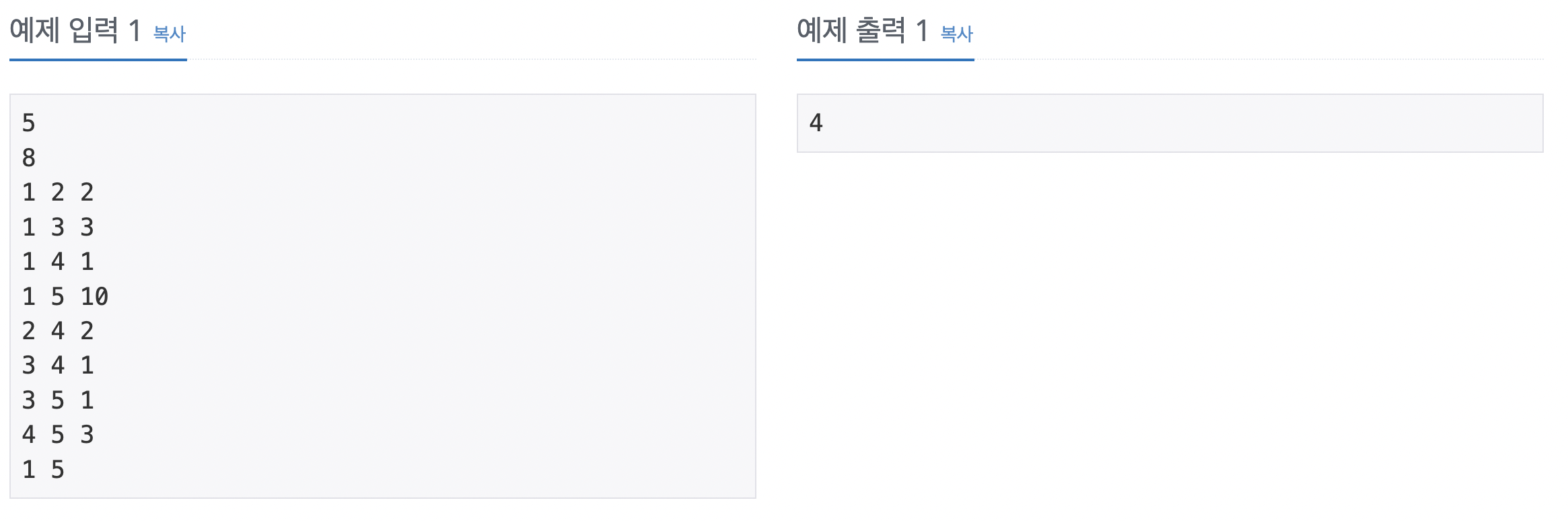
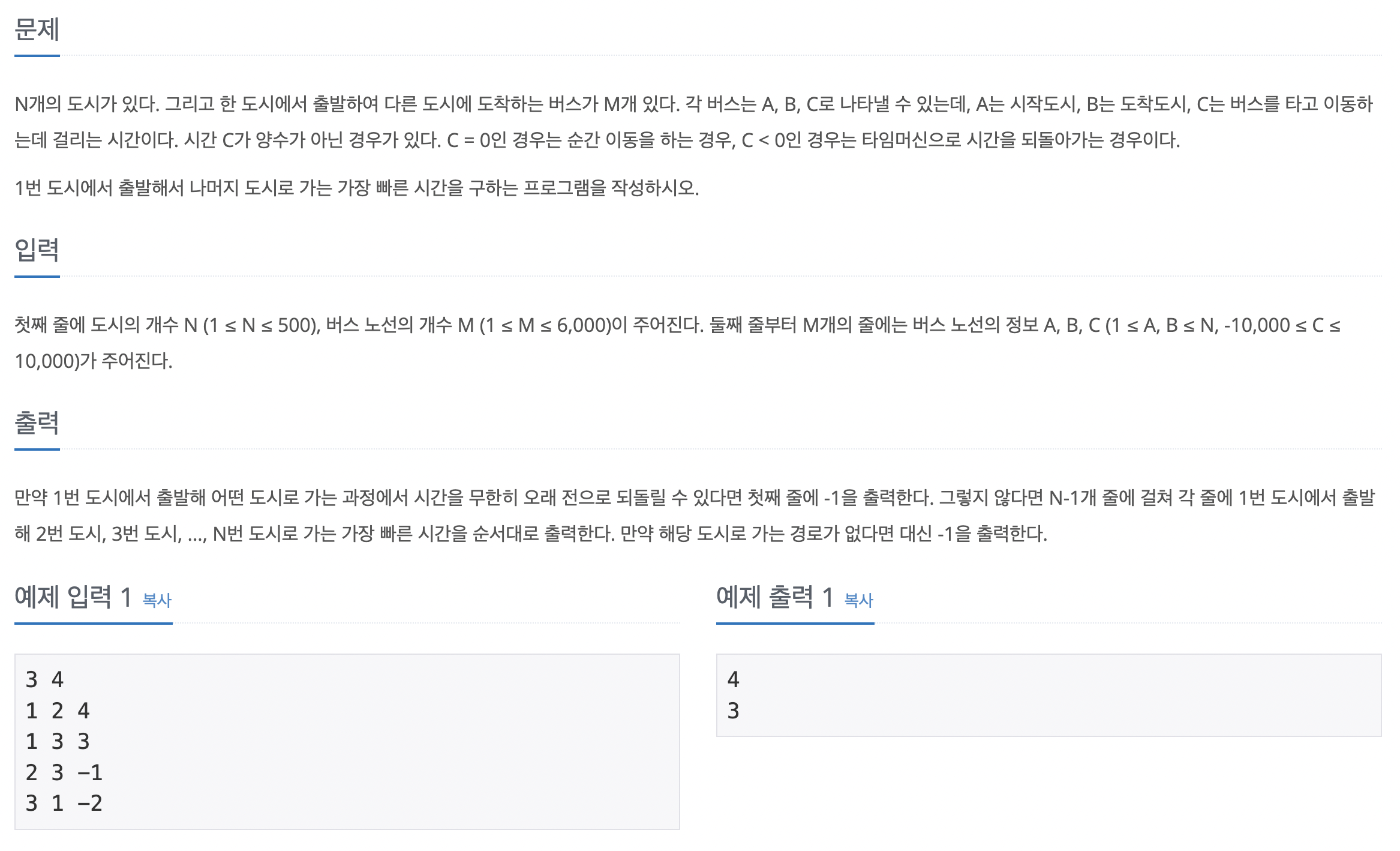
집합 S에 속해있는 단어들을 이용해 트라이 구조를 생성하고, 트라이 검색을 이용해 문자열 M개의 포함 여부를 카운트하는 전형적인 트라이 자료구조 문제이다. 트라이 자료구조를 생성하고 현재 문자열을 가리키는 위치의 노드가 공백 상태라면 신규 노드를 생성하고 아니라면 이동한다. 문자열 마지막에 도달하면 리프 노드라고 표시한다. 트라이 자료구조 검색으로 집합 S에 포함된 문자열을 센다. 부모-자식 관계를 이용해 대상 문자열을 검색했을 때 문자열이 끝날 때까지 공백 상태가 없고, 현재 문자의 마지막 노드가 트라이의 리프 노드라면 이 문자를 집합 S에 포함된 문자열로 센다.
정확한 풀이
import java.io.*;
import java.util.*;
public class Baek14425 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
dNode root = new dNode();
while(n > 0) { // 트라이 자료구조 구축하기
String text = br.readLine();
dNode now = root;
for(int i = 0; i < text.length(); i++) {
char c = text.charAt(i);
// 26개 알파벳의 위치를 배열 index로 나타내기 위해 -'a' 수행하기
if(now.next[c - 'a'] == null) {
now.next[c - 'a'] = new dNode();
}
now = now.next[c - 'a'];
if(i == text.length() - 1) {
now.isEnd = true;
}
}
n--;
}
int count = 0;
while(m > 0) { // 트라이 자료구조 검색하기
String text = br.readLine();
dNode now = root;
for(int i = 0; i < text.length(); i++) {
char c = text.charAt(i);
if(now.next[c - 'a'] == null) { // 공백 노드라면 이 문자열을 포함하지 않음
break;
}
now = now.next[c - 'a'];
if(i == text.length() - 1 && now.isEnd) { // 문자열의 끝이고 현재까지 모두 일치하면
count++; // S 집합에 포함되는 문자열
}
}
m--;
}
System.out.println(count);
}
}
class dNode {
dNode[] next = new dNode[26];
boolean isEnd; // 문자열의 마지막 유무를 표시하기
}
오늘의 회고
오늘은 트라이 자료구조를 배우고 트라이 문제를 풀었습니다. 1문제 밖에 풀지 못했습니다. 장마라 밖에 비도 많이 오고 날씨도 우중충한데 퍼지지 않고 공부하겠습니다.
'알고리즘 > 알고리즘 문제풀이' 카테고리의 다른 글
| Do it! 알고리즘 코딩 테스트 (76번 ~ 77번) (0) | 2022.06.27 |
|---|---|
| Do it! 알고리즘 코딩 테스트 (70번) (0) | 2022.06.24 |
| Do it! 알고리즘 코딩 테스트 (67번 ~ 68번) (0) | 2022.06.22 |
| Do it! 알고리즘 코딩 테스트 (64번 ~ 66번) (0) | 2022.06.21 |
| 백준) 문자열 (0) | 2022.06.21 |