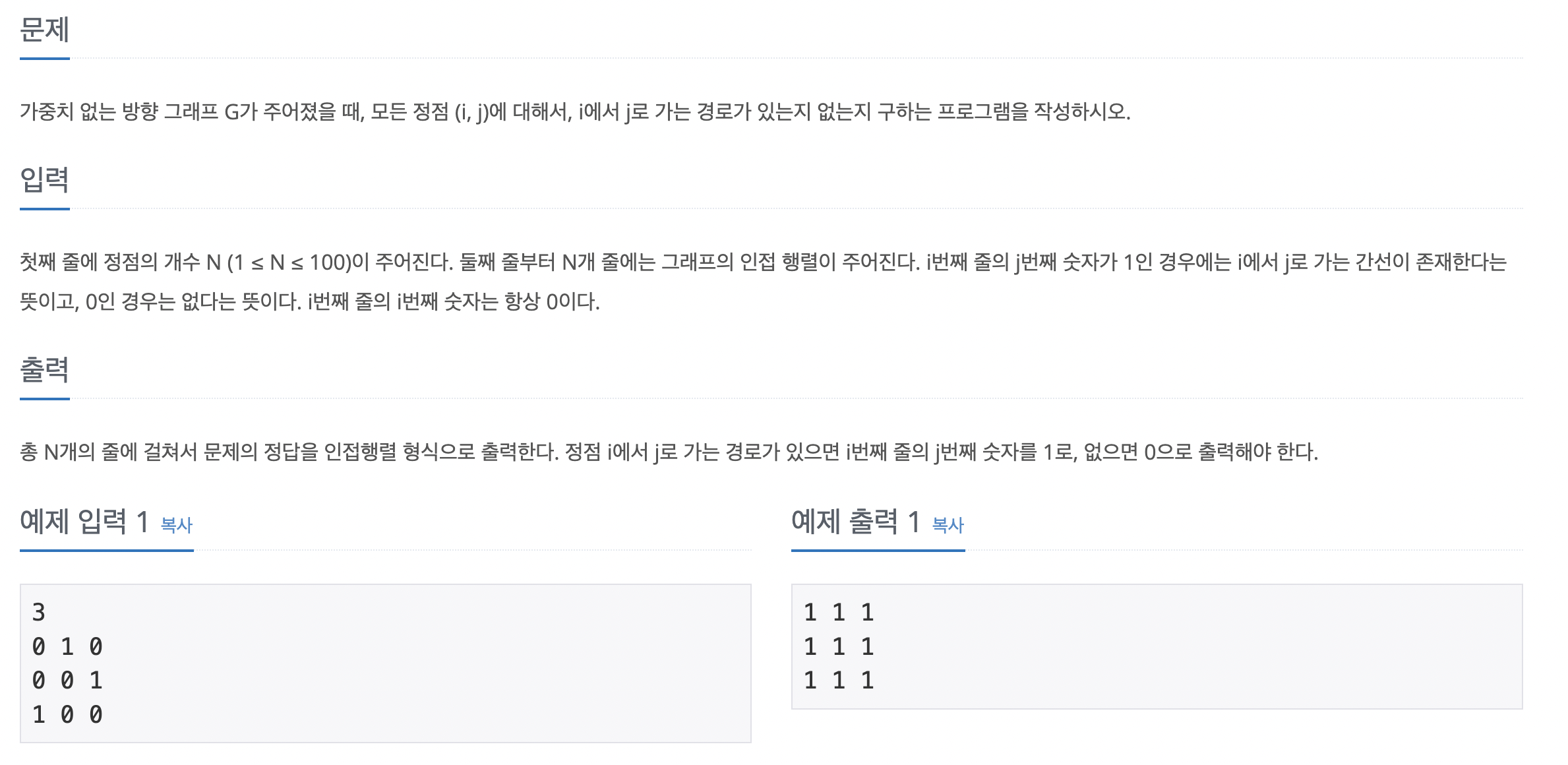
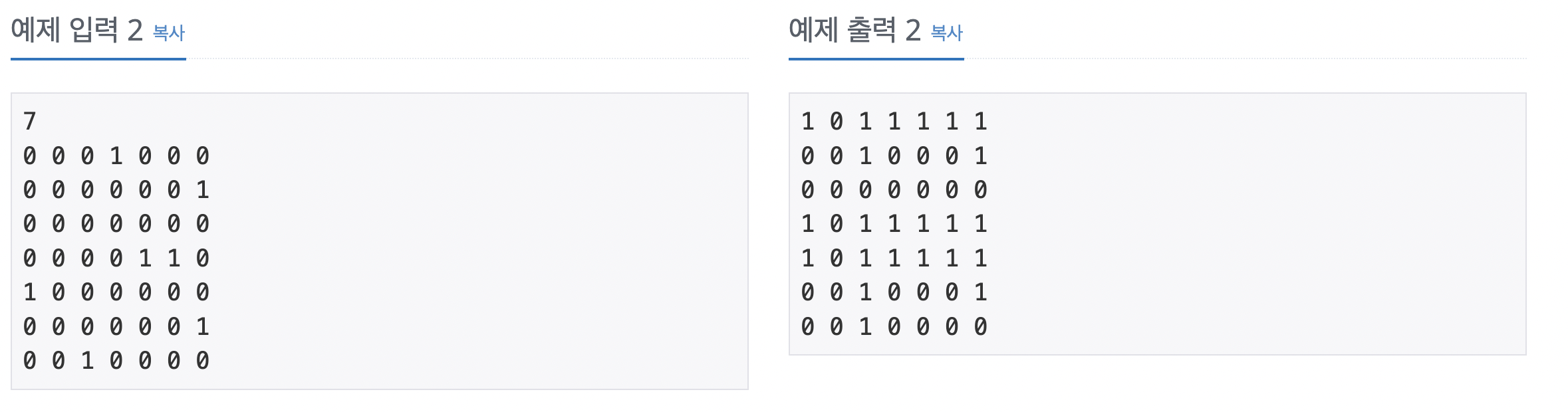
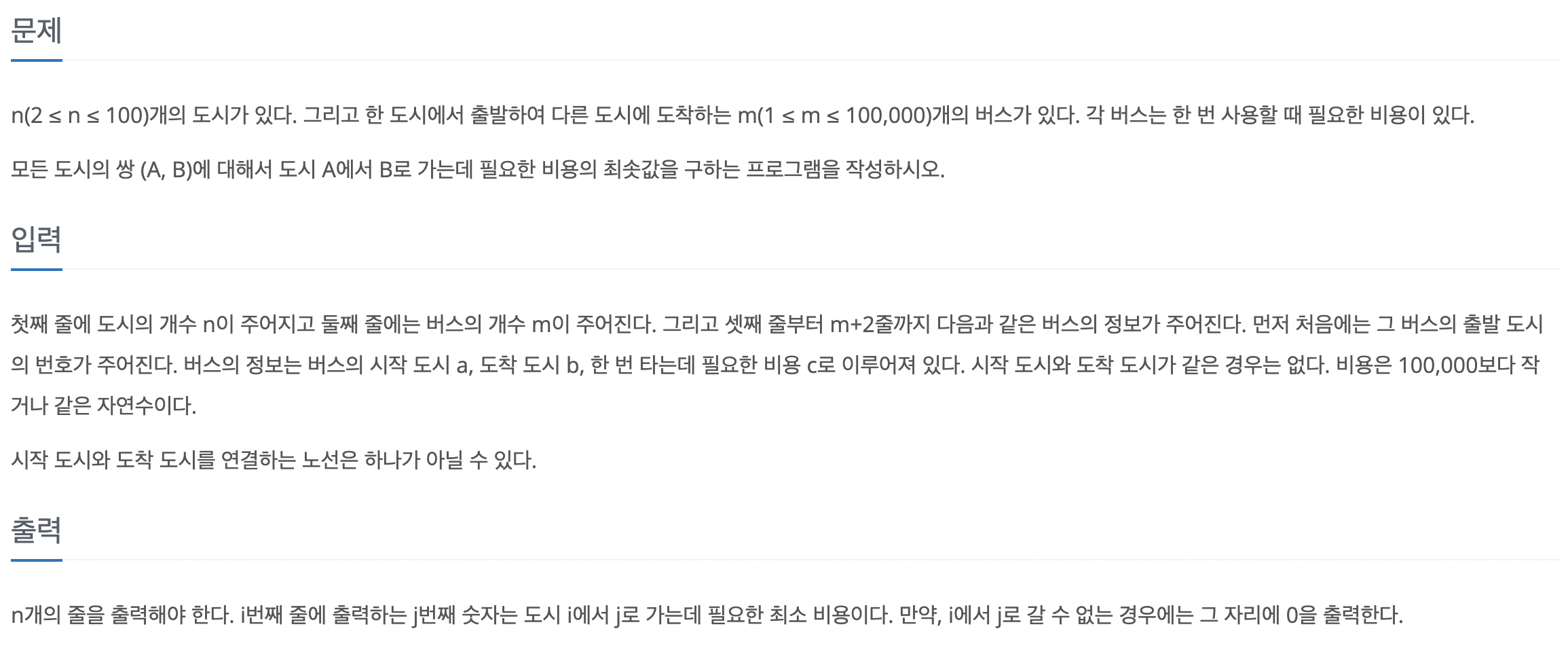
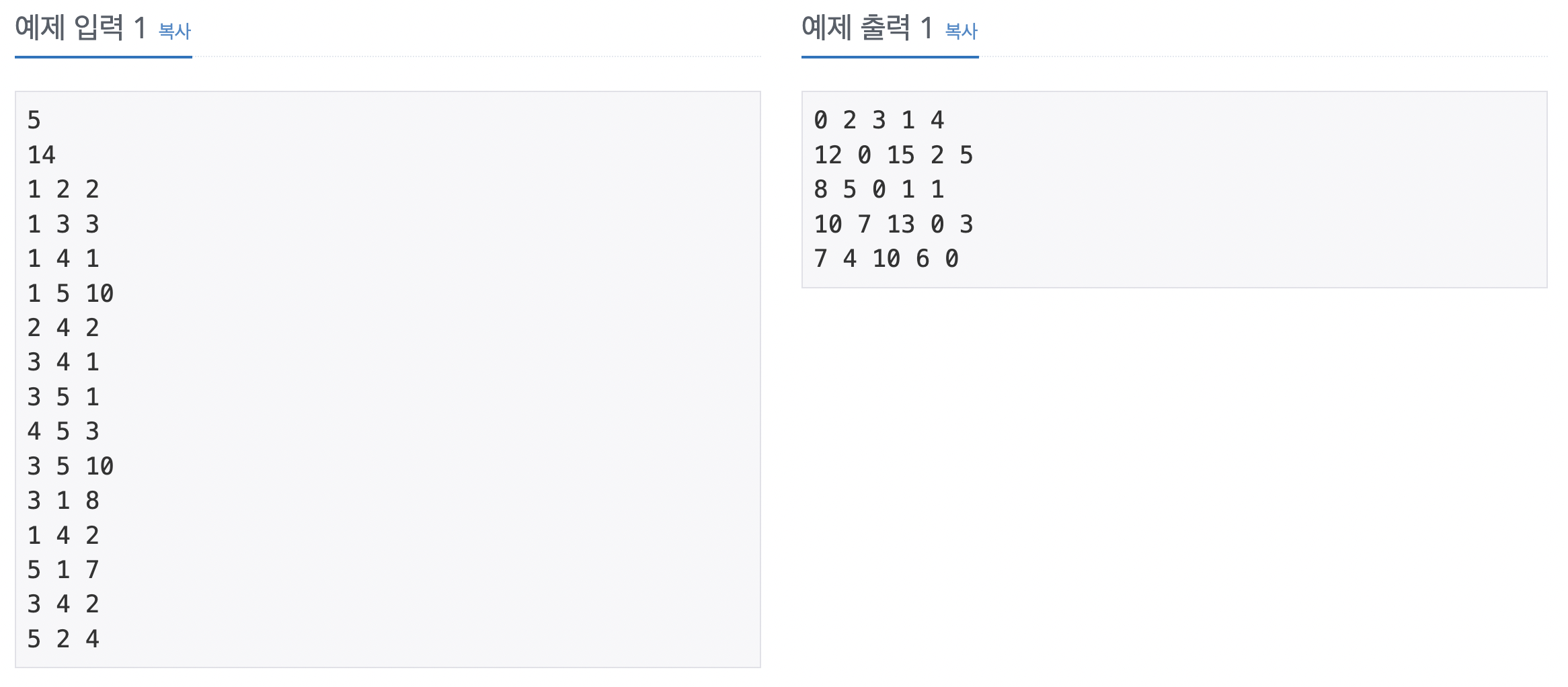
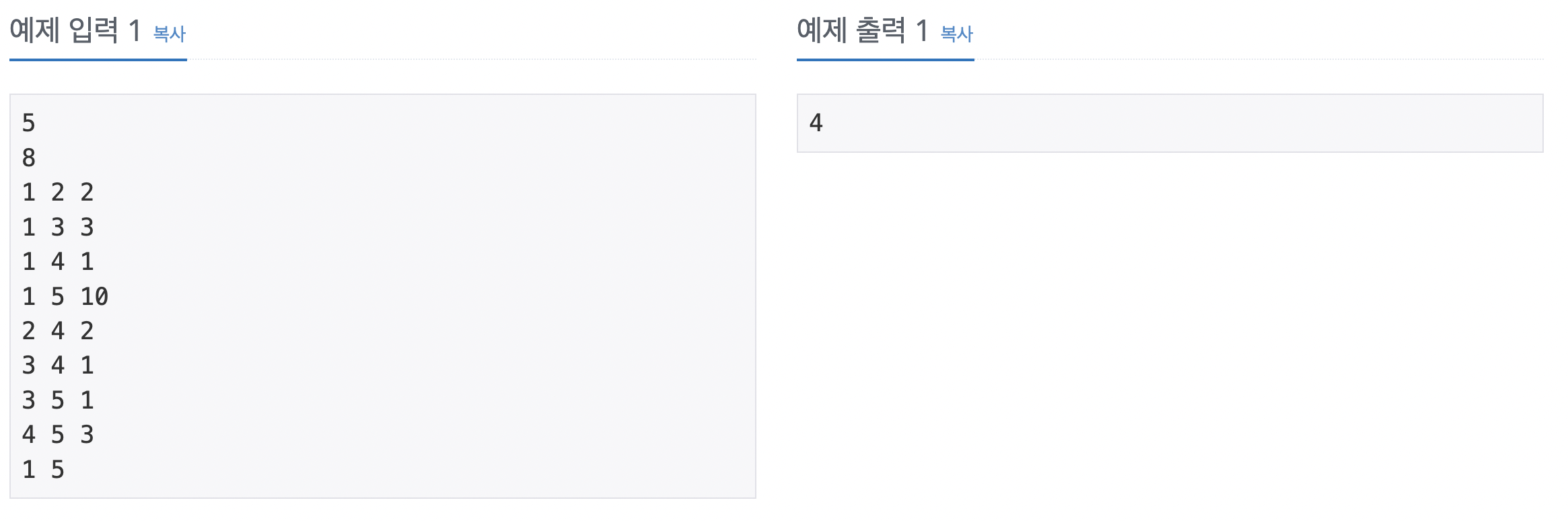
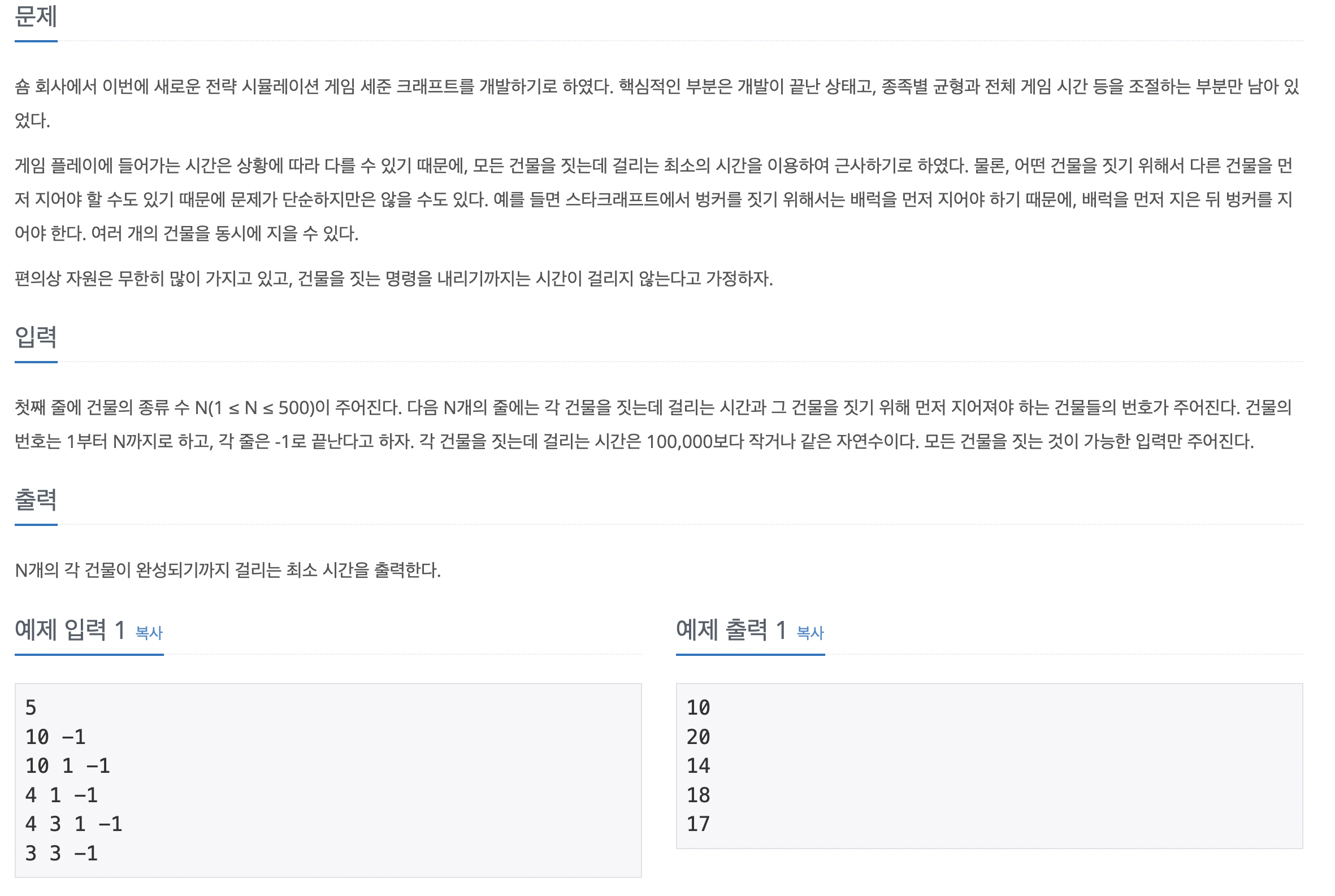
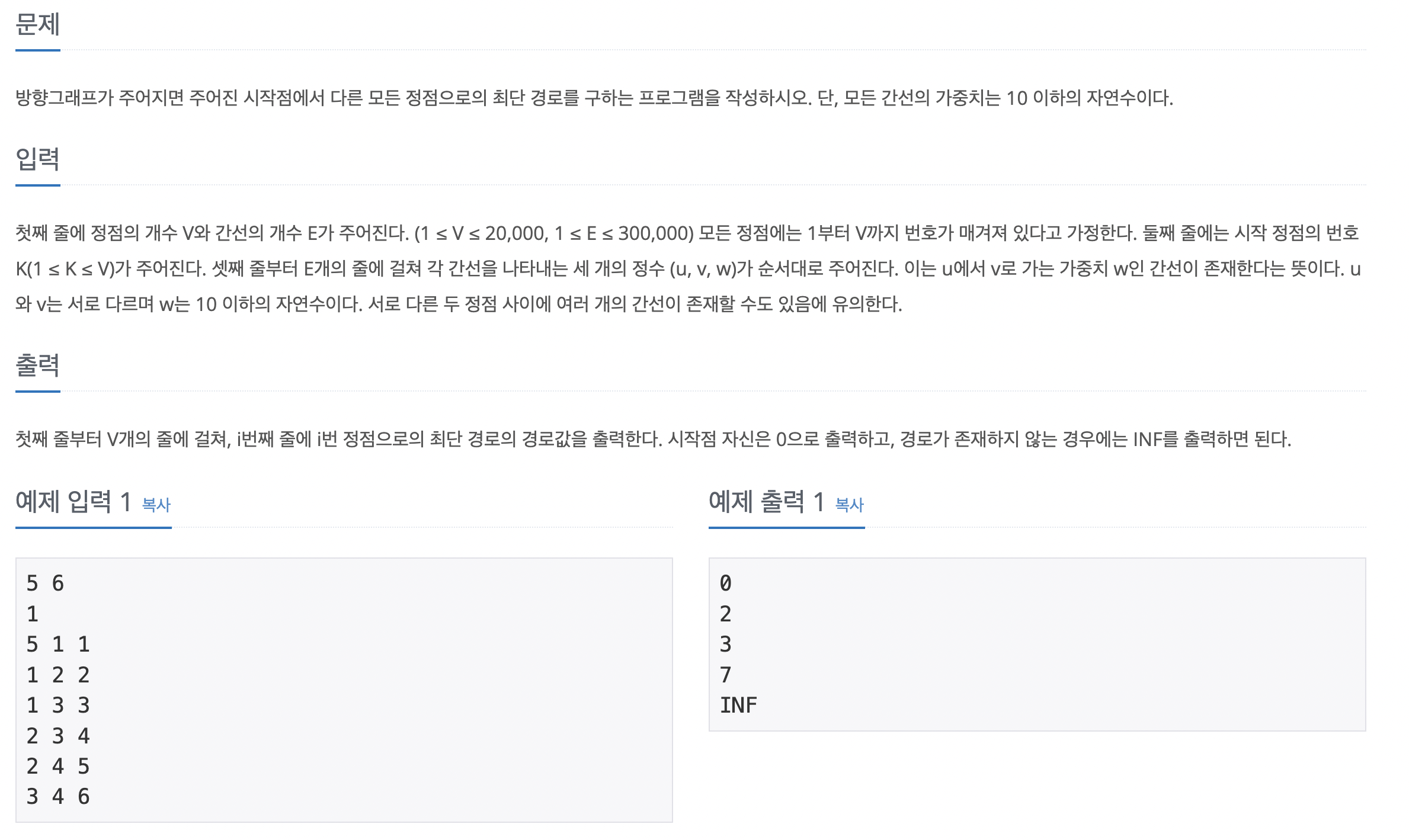
64번 최소 스패닝 트리

내가 떠올린 풀이 해설
에지 리스트에 에지 정보를 저장한 후 부모 노드를 초기화한다. 사이클 생성 유무를 판단하기 위한 파인드용 부모 노드도 초기화한다. 크루스칼 알고리즘을 수행한다. 현재 미사용 에지 중 가중치가 가장 작은 에지를 선택하고, 이 에지를 연결했을 때 사이클의 발생 유무를 판단한다. 사이클이 발생하면 생략하고, 발생하지 않으면 에지 값을 더한다. 에지를 더한 횟수가 V(노드 개수) - 1 이 될 때까지 반복하고, 반복이 끝나면 에지의 가중치를 모두 더한 값을 출력한다.
정확한 풀이
import java.io.*;
import java.util.*;
public class Baek1197 {
static PriorityQueue<pEdge> que;
static int[] parent;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
parent = new int[n + 1];
que = new PriorityQueue<>();
for(int i = 0; i < n; i++) {
parent[i] = i;
}
for(int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
que.add(new pEdge(a, b, c));
}
int useEdge = 0;
int result = 0;
while(useEdge < n - 1) {
pEdge now = que.poll();
if(find(now.a) != find(now.b)) { // 같은 부모가 아니라면 연결해도 사이클이 생기지 않음
union(now.a, now.b);
result = result + now.c;
useEdge++;
}
}
System.out.println(result);
}
private static void union(int a, int b) {
a = find(a);
b = find(b);
if(a != b) {
parent[b] = a;
}
}
private static int find(int a) {
if(a == parent[a]) {
return a;
}
else {
return parent[a] = find(parent[a]);
}
}
}
class pEdge implements Comparable<pEdge>{
int a;
int b;
int c;
public pEdge(int a, int b, int c) {
this.a = a;
this.b = b;
this.c = c;
}
@Override
public int compareTo(pEdge o) {
return this.c - o.c;
}
}
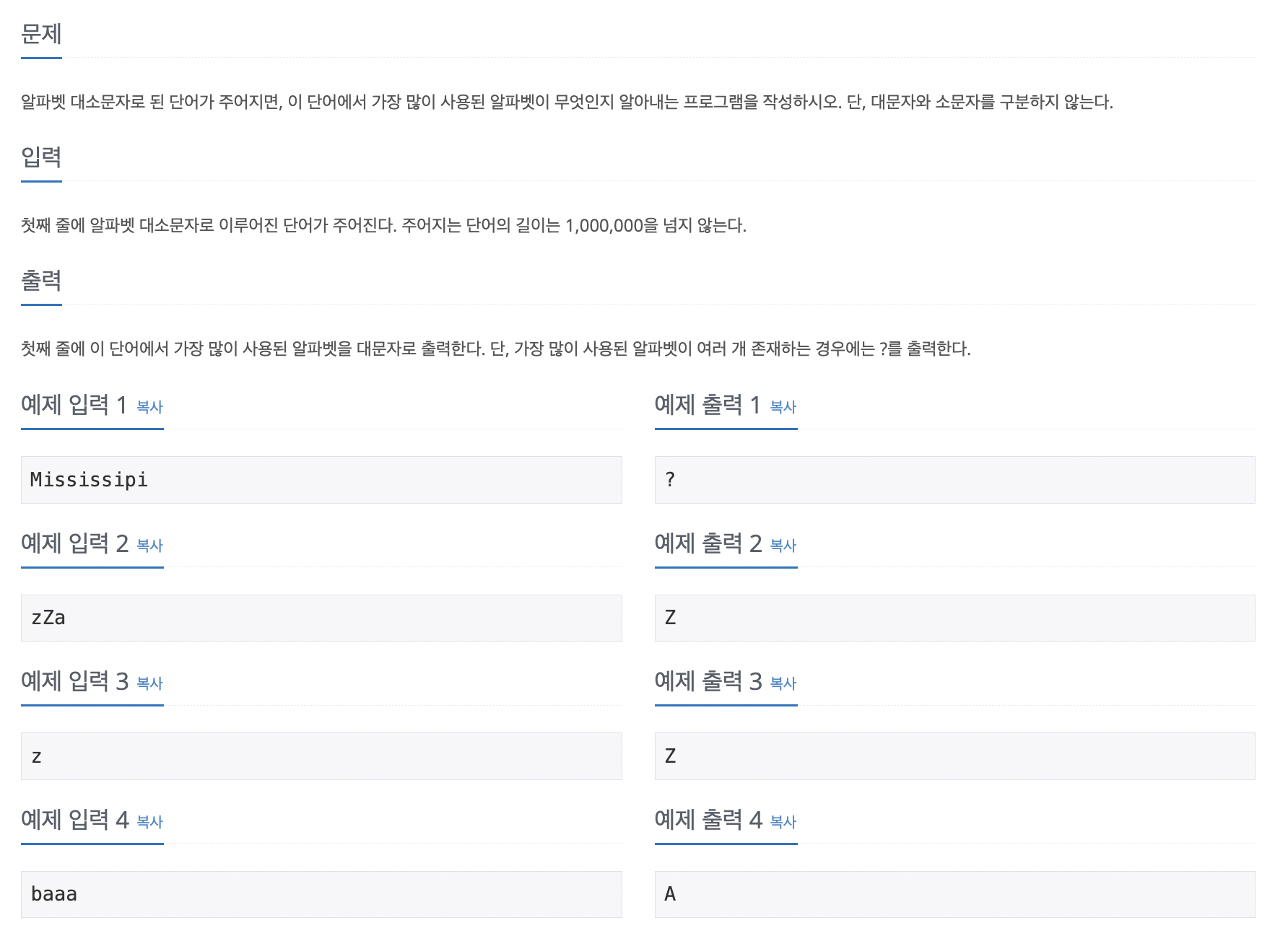
66번 블우이웃 돕기


내가 떠올린 풀이 해설
인접 행렬의 형태로 데이터가 들어오기 때문에 이 부분을 최소 신장 트리가 가능한 형태로 변형하는 것이 이 문제의 핵심이다. 먼저 문자열로 주어진 랜선의 길이를 숫자로 변형해 랜선의 총합을 저장한다. 이때 i와 j가 같은 곳의 값은 같은 컴퓨터를 연결한다는 의미이므로 별도 에지로 저장하지 않고 나머지 위치의 값들을 i -> j로 가는 에지로 생성하고, 에지 리스트에 저장하면 최소 신장 트리로 변형할 수 있다.
입력 데이터의 정보를 배열에 저장한다. 먼저 입력으로 주어진 문자열을 숫자로 변환해 총합으로 저장한다. 소문자는 현재 문자 - 'a' + 1, 대문자는 현재 문자 - 'A' + 27 변환한다. i와 j가 다른 경우에는 다른 컴퓨터를 연결하는 랜선이므로 에지리스트에 저장한다. 저장된 에지 리스트를 바탕으로 최소 신장 트리 알고리즘을 수행한다. 최소 신장 트리의 결괏값이 다솜이가 최소한으로 필요한 렌선의 길이이므로 처음 저장해 둔 랜선의 총합에서 최소 신장 트리의 결괏값을 뺀 값을 정답으로 출력한다. 최소 신장 트리에서 사용한 에지 개수가 n - 1이 아닌 경우에는 모든 컴퓨터를 연결할 수 없다는 의미이므로 -1을 출력한다.
정확한 풀이
import java.io.*;
import java.util.*;
public class Baek1414 {
static int n, sum;
static PriorityQueue<lEdge> que;
static int[] parent;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
que = new PriorityQueue<>();
for(int i = 0; i < n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
char[] tmpc = st.nextToken().toCharArray();
for(int j = 0; j < n; j++) {
int tmp = 0;
if(tmpc[j] >= 'a' && tmpc[j] <= 'z') {
tmp = tmpc[j] - 'a' + 1;
}
else if(tmpc[j] >= 'A' && tmpc[j] <= 'Z') {
tmp = tmpc[j] - 'A' + 27;
}
sum = sum + tmp;
if(i != j && tmp != 0) {
que.add(new lEdge(i, j, tmp));
}
}
}
parent = new int[n];
for(int i = 0; i < n; i++) {
parent[i] = i;
}
int useEdge = 0;
int result = 0;
while(!que.isEmpty()) {
lEdge now = que.poll();
if(find(now.s) != find(now.e)) {
union(now.s, now.e);
result = result + now.v;
useEdge++;
}
}
if(useEdge == n - 1) {
System.out.println(sum - result);
}
else {
System.out.println(-1);
}
}
private static void union(int s, int e) {
s = find(s);
e = find(e);
if(s != e) {
parent[e] = s;
}
}
private static int find(int s) {
if(s == parent[s]) {
return s;
}
else {
return parent[s] = find(parent[s]);
}
}
}
class lEdge implements Comparable<lEdge> {
int s;
int e;
int v;
public lEdge(int s, int e, int v) {
this.s = s;
this.e = e;
this.v = v;
}
@Override
public int compareTo(lEdge o) {
return this.v - o.v;
}
}
오늘의 회고
오늘은 최소 신장 트리 문제 2문제를 풀었습니다. 코드를 구현하는데 어려웠습니다. 반복해서 제가 직접 구현할 수 있게 만들겠습니다. 오늘 날씨가 너무 더운데 모든 취준생분들 화이팅입니다. 열심히 나아가겠습니다. 모두 화이팅입니다.
'알고리즘 > 알고리즘 문제풀이' 카테고리의 다른 글
| Do it! 알고리즘 코딩 테스트 (69번) (0) | 2022.06.23 |
|---|---|
| Do it! 알고리즘 코딩 테스트 (67번 ~ 68번) (0) | 2022.06.22 |
| 백준) 문자열 (0) | 2022.06.21 |
| 백준) HashMap (0) | 2022.06.18 |
| Do it! 알고리즘 코딩 테스트 (62번 ~ 63번) (0) | 2022.06.17 |