57번 최소비용 구하기

내가 떠올린 풀이 해설
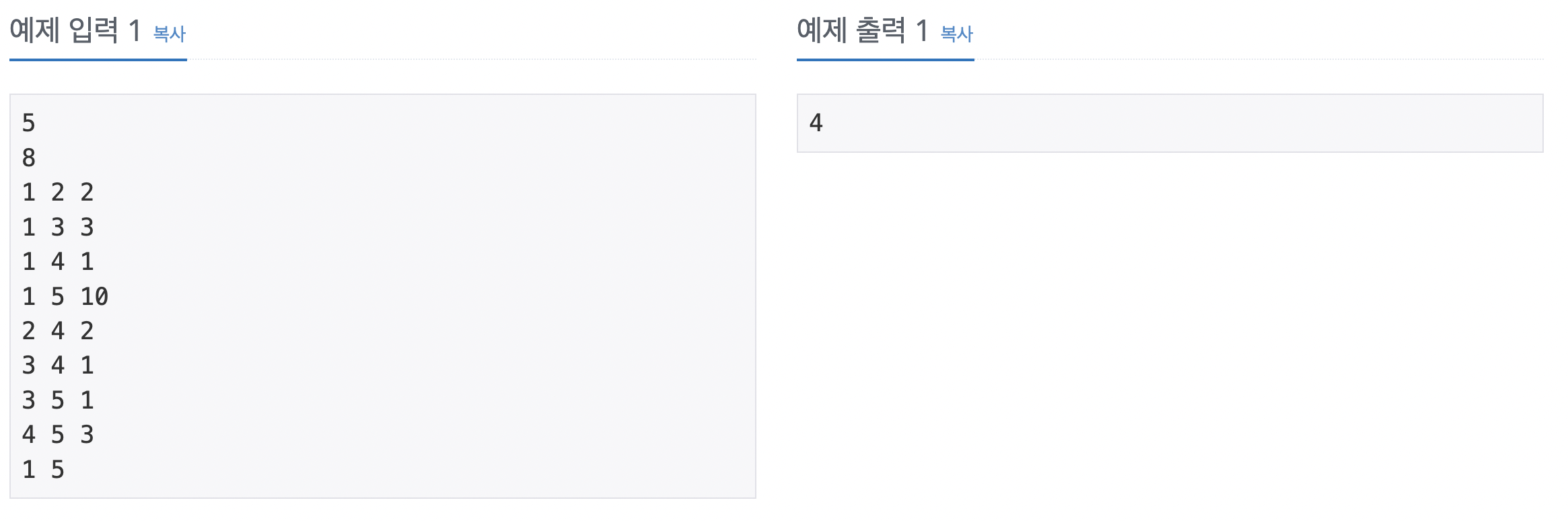
버스의 비용의 범위가 음수가 아니기 때문에 이 문제는 다익스트라 알고리즘을 이용해 해결할 수 있다. 도시의 개수가 최대 1,000개 이므로 인접 행렬 방식으로 해결할 수 있지만 인접 리스트로 풀었다. 도시는 노드, 도시 간 버스 비용은 에지로 나타낸다.
도시 개수의 크기만큼 인접 리스트 배열의 크기를 설정한다. 이때 버스의 비용이 존재하므로 인접 리스트 배열의 자료형이 될 클래스를 선언한다. 그리고 버스 개수의 크기만큼 반복문을 돌면서 그래프를 리스트 배열에 저장한다. 다익스트라 알고리즘을 수행한다. 최단 거리를 완성되면 출력한다.
정확한 풀이
import java.io.*;
import java.util.*;
public class Baek1916 {
static int n, m;
static ArrayList<Node>[] list;
static boolean[] visit;
static int[] distance;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st;
n = Integer.parseInt(br.readLine());
m = Integer.parseInt(br.readLine());
list = new ArrayList[n + 1];
visit = new boolean[n + 1];
distance = new int[n + 1];
for(int i = 0; i <= n; i++) {
list[i] = new ArrayList<Node>();
}
for(int i = 0; i <= n; i++) {
distance[i] = Integer.MAX_VALUE;
}
for(int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int s = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
list[s].add(new Node(e, v));
}
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
dijkstra(start, end);
System.out.println(distance[end]);
}
private static int dijkstra(int start, int end) {
PriorityQueue<Node> que = new PriorityQueue<>();
que.offer(new Node(start, 0));
distance[start] = 0;
while(!que.isEmpty()) {
Node cur = que.poll();
int c_v = cur.vertex;
if(!visit[c_v]) {
visit[c_v] = true;
for(Node n : list[c_v]) {
if(!visit[n.vertex] && distance[n.vertex] > distance[c_v] + n.value) {
distance[n.vertex] = distance[c_v] + n.value;
que.add(new Node(n.vertex, distance[n.vertex]));
}
}
}
}
return distance[end];
}
}
class Node implements Comparable<Node>{
int vertex;
int value;
public Node(int vertex, int value) {
this.vertex = vertex;
this.value = value;
}
@Override
public int compareTo(Node o) {
return value - o.value;
}
}
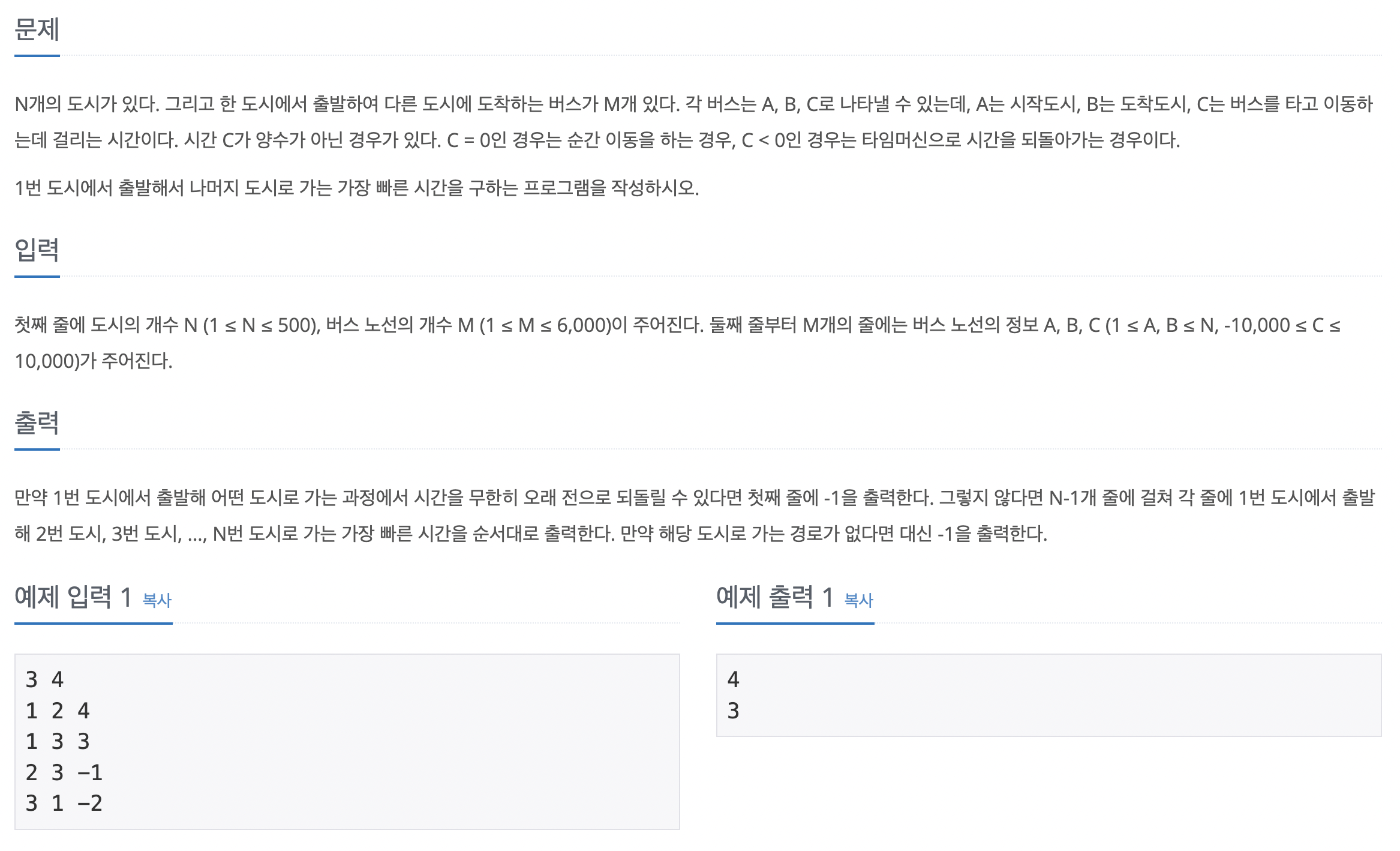
59번 타임머신
내가 떠올린 풀이
에지 리스트에 에지 데이터를 저장한 후 거리 배열을 초기화한다. 최초 시작점에 해당하는 거리 배열값은 0으로 초기화한다. 벨만-포드 알고리즘을 수행한다. 음수 사이클이 존재하면 -1, 존재하지 않으면 거리 배열의 값을 출력한다. 단, 거리 배열의 값이 INF일 경우에는 -1을 출력한다.
벨만-포드 수행과정
1. 모든 에지와 관련된 정보를 가져온 후 다음 조건에 따라 거리 배열의 값을 업데이트한다.
- 출발 노드가 방문한 적이 없는 노드(출발 노드 거리 == INF)일 때 값을 업데이트하지 않는다.
- 출발 노드의 거리 배열값 + 에지 가중치 < 종료 노드의 거리 배열 값일 때 종료 노드의 거리 배열 값을 업데이트한다.
2. 노드 개수 -1번만큼 1번을 반복한다.
3. 음수 사이클 유무를 알기 위해 모든 에지에 관해 다시 한번 1번을 수행한다. 이때 한 번이라도 값이 업데이트되면 음수 사이클이 존재한다고 판단한다.
정확한 풀이
import java.io.*;
import java.util.*;
public class Baek11657 {
static int n, m;
static long distance[];
static Edge edges[];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
edges = new Edge[m + 1];
distance = new long[n + 1];
for(int i = 0; i <= n; i++) {
distance[i] = Integer.MAX_VALUE;
}
for(int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int s = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
edges[i] = new Edge(s, e, v);
}
distance[1] = 0;
for(int i = 1; i < n; i++) {
for(int j = 0; j < m; j++) {
Edge edge = edges[j];
if(distance[edge.s] != Integer.MAX_VALUE
&& distance[edge.e] > distance[edge.s] + edge.v) {
distance[edge.e] = distance[edge.s] + edge.v;
}
}
}
boolean mCycle = false;
for(int i = 0; i < m; i++) {
Edge edge = edges[i];
if(distance[edge.s] != Integer.MAX_VALUE
&& distance[edge.e] > distance[edge.s] + edge.v) {
mCycle = true;
}
}
if(!mCycle) {
for(int i = 2; i <= n; i++) {
if(distance[i] == Integer.MAX_VALUE) {
System.out.println("-1");
}
else {
System.out.println(distance[i]);
}
}
}
else {
System.out.println("-1");
}
}
}
class Edge {
int s;
int e;
int v;
public Edge(int s, int e, int v) {
this.s = s;
this.e = e;
this.v = v;
}
}
오늘의 회고
오늘은 다익스트라 한 문제와 벨만-포드 알고리즘 개념과 관련된 문제를 풀었습니다. 아직 다익스트라와 벨만-포드 구현에 대해 많이 부족한 것 같습니다. 내일도 이와 관련된 문제들을 풀고 다시 한번 개념에 대해 공부하겠습니다.
'알고리즘 > 알고리즘 문제풀이' 카테고리의 다른 글
| Do it! 알고리즘 코딩 테스트 (62번 ~ 63번) (0) | 2022.06.17 |
|---|---|
| Do it! 알고리즘 코딩 테스트 (61번) (0) | 2022.06.16 |
| Do it! 알고리즘 코딩 테스트 (54번 ~ 56번) (0) | 2022.06.14 |
| Do it! 알고리즘 코딩 테스트 (52번 ~ 53번) (0) | 2022.06.13 |
| Do it! 알고리즘 코딩 테스트 (51번) (0) | 2022.06.10 |