62번 경로 찾기
내가 떠올린 풀이 해설
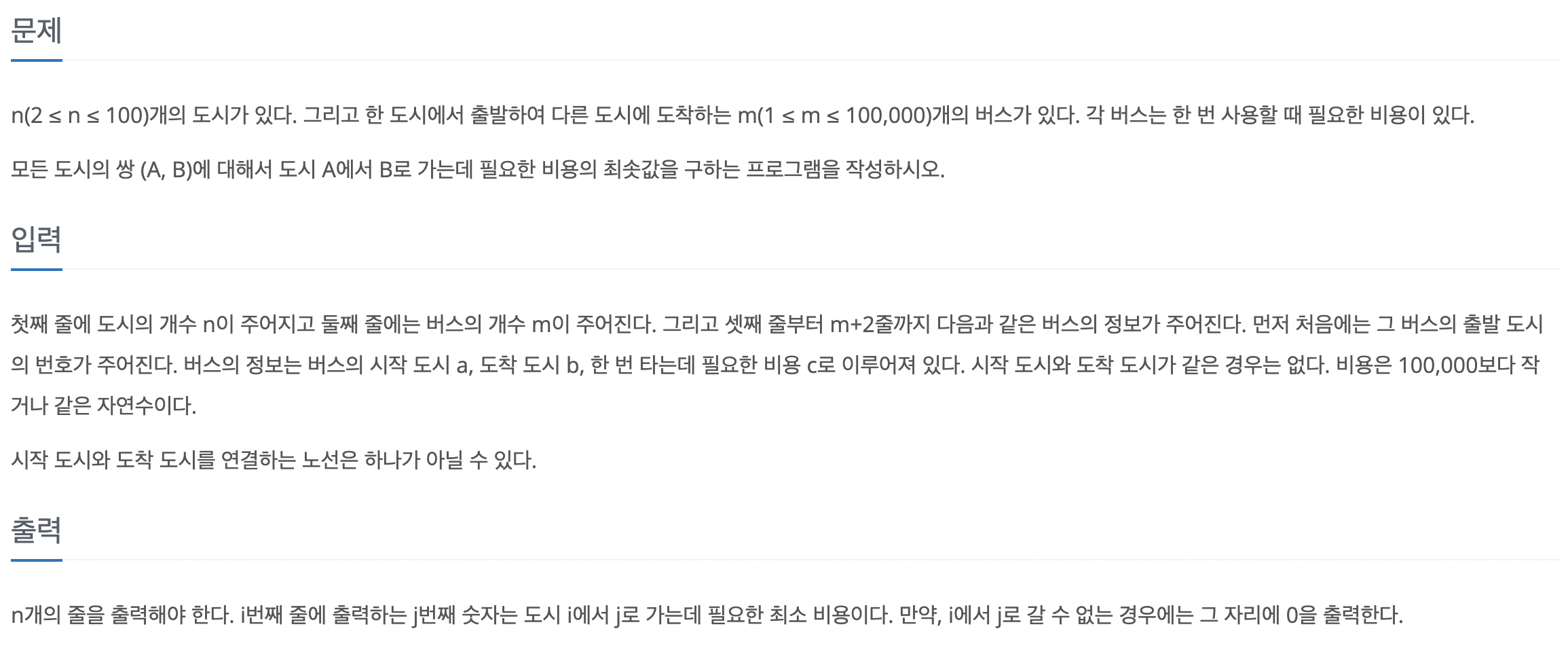
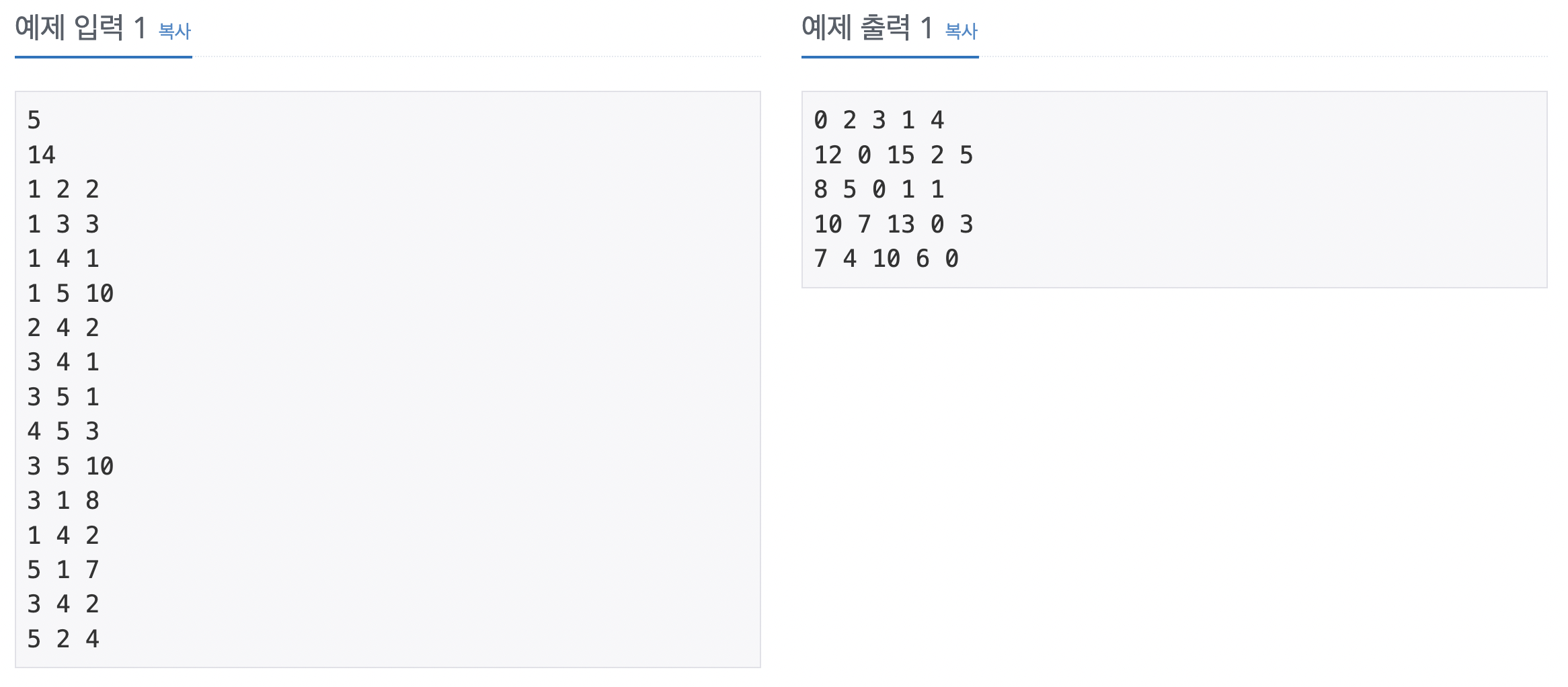
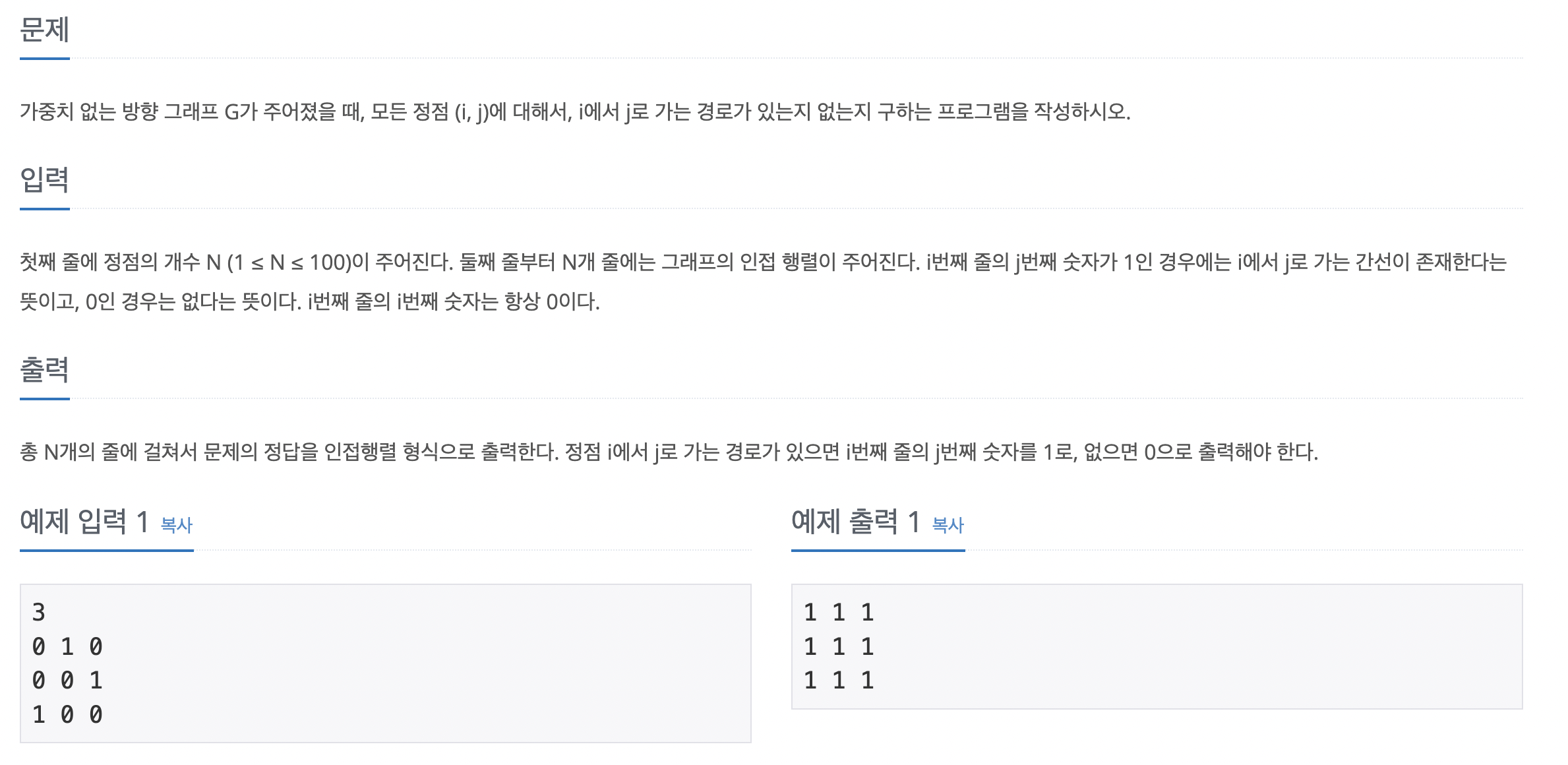
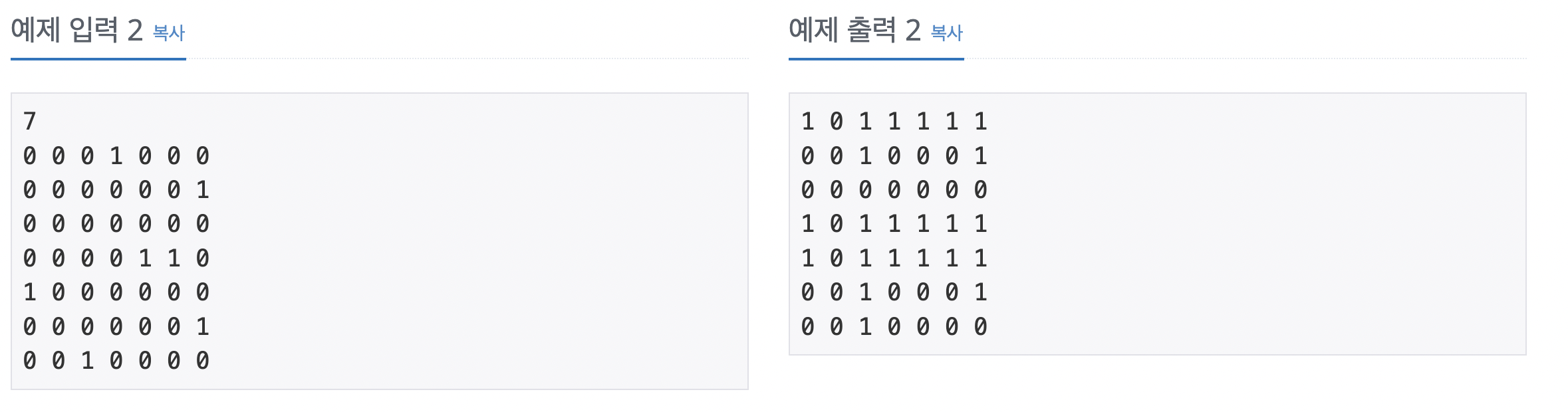
어제 배운 플로이드-위셜 기본 문제이다. 모든 노드 쌍에 관해 경로가 있는지 여부를 확인하는 방법은 플로이드-위셜 알고리즘을 수행해 결과 배열을 그대로 출력하면 된다. 입력 데이터를 인접 행렬에 저장한다. s와 e가 모든 중간 경로(k) 중 1개라도 연결돼 있다면 s와 e는 연결 노드로 저장한다. 변경된 인접 행렬을 출력한다.
정확한 풀이
import java.io.*;
import java.util.*;
public class Baek11403 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[][] arr = new int[n + 1][n + 1];
for(int i = 1; i <= n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
for(int j = 1; j <= n; j++) {
arr[i][j] = Integer.parseInt(st.nextToken());
}
}
for(int k = 1; k <=n; k++) {
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
if(arr[i][k] == 1 && arr[k][j] == 1) {
arr[i][j] = 1;
// k를 거치는 모든 경로 중 1개라도 연결돼 있는 경로가 있다면 i와 j는 연결 노드로 취급
}
}
}
}
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
System.out.print(arr[i][j] + " ");
}
System.out.println();
}
}
}63번 케빈 베이컨의 6단계 법칙


내가 떠올린 풀이 해설
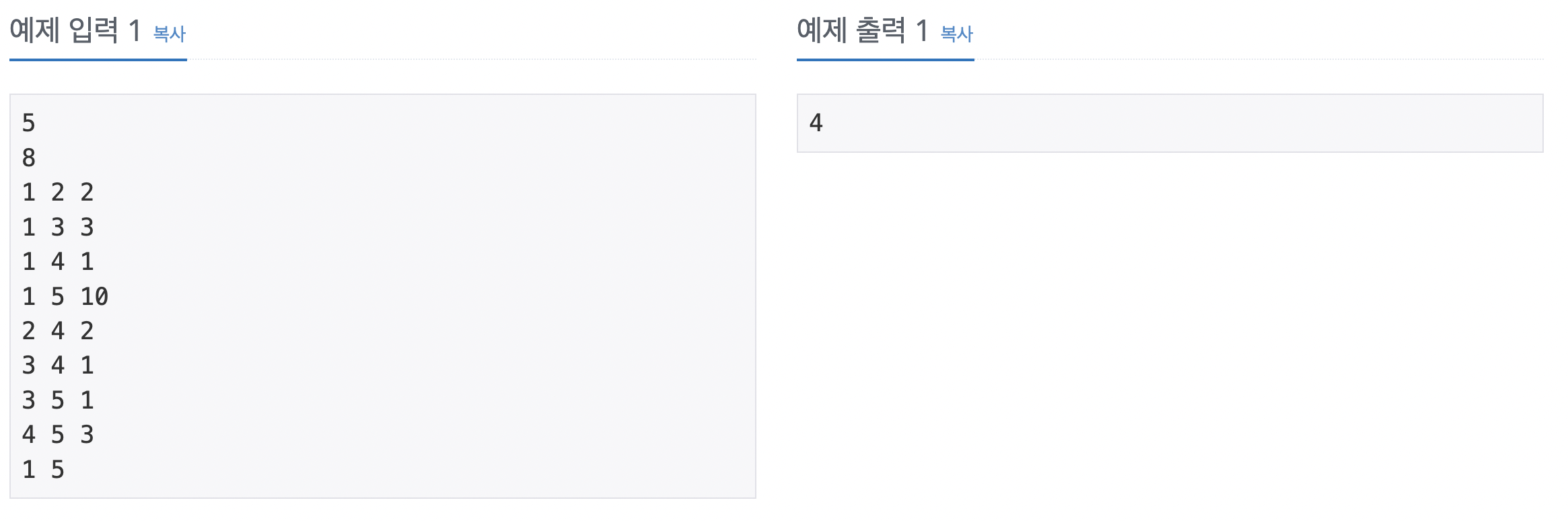
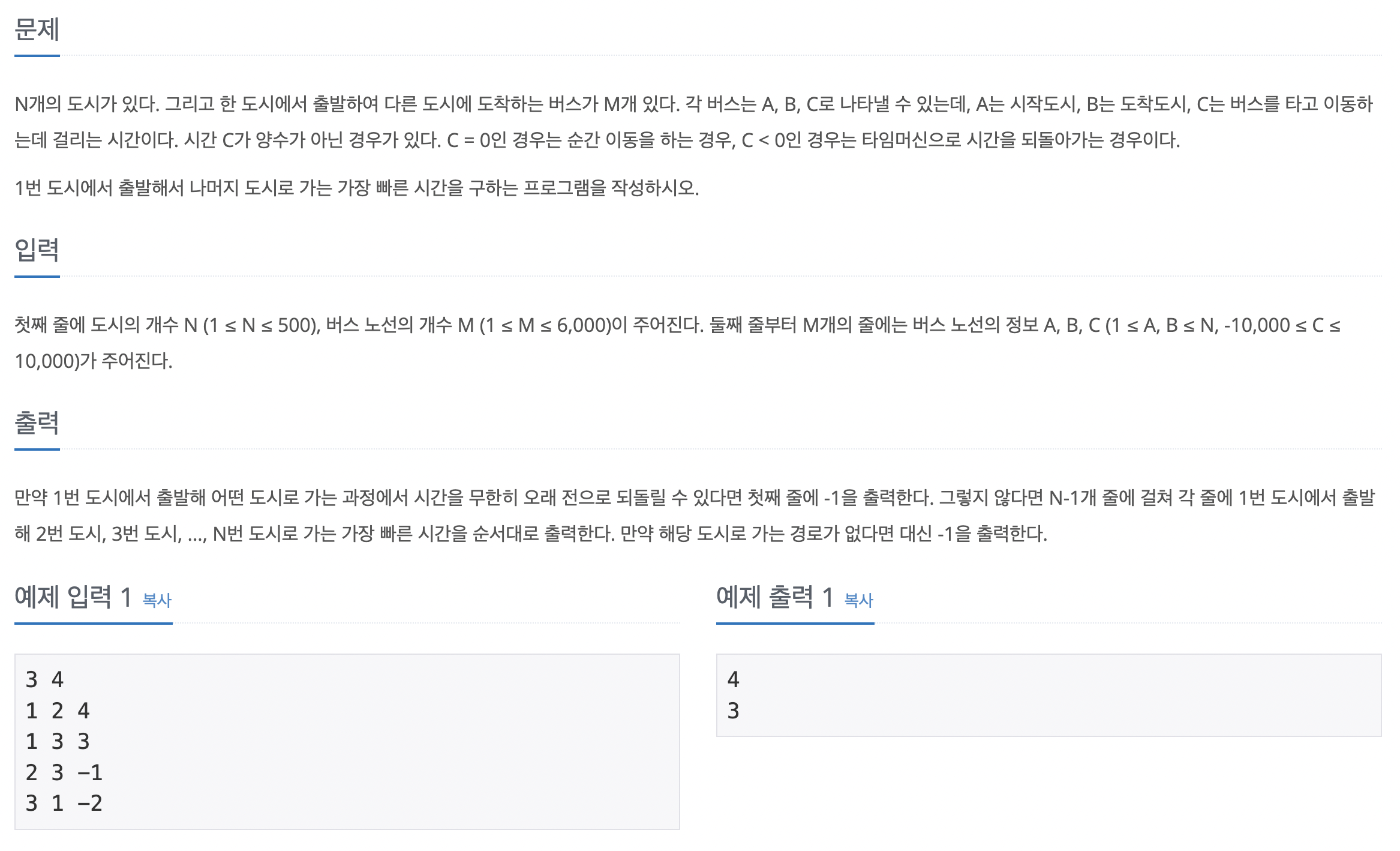
BFS를 이용해서도 풀 수 있는 문제이다. 이 문제를 풀기 위해 몇가지 아이디어가 필요하다. 1번째로 사람들이 직접적인 친구 관계를 맺은 상태를 비용 1로 계산하는 것이다. 즉 가중치를 1로 정한 후 인접 행렬에 저장한다는 의미이다. 또한 플로이드-위셜은 모든 쌍과 관련된 최단 경로이므로 한 row의 배열 값은 이 row의 index값에서 다른 모든 노드와 관련된 최단 경로를 나타낸다고 볼 수 있다. 즉 i번째 row의 합이 i번째 사람의 케빈 베이컨의 수가 된다는 뜻이다.
먼저 인접 행렬을 생성한 후, 자기 자신이면 0, 아니면 충분히 큰 수로 인접 행렬의 값을 초기화한다. 그리고 친구 관계 정보를 인접 행렬에 저장한다. i와 j가 친구라면 arr[i][j] = 1, arr [j][i] = 1로 값을 업데이트한다. 플로이드-위셜 3중 for문으로 모든 중간 경로를 탐색한다. 케빈 베이컨의 수를 비교해 가장 작은 수가 나온 행 번호를 정답으로 출력한다. 같은 수가 있을 때는 더 작은 행 번호를 출력한다.
정확한 풀이
import java.io.*;
import java.util.*;
public class Baek1389 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
int[][] arr = new int[n + 1][n + 1];
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
if(i == j) {
arr[i][j] = 0;
}
else {
arr[i][j] = 1000001;
}
}
}
for(int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int s = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
arr[s][e] = 1;
arr[e][s] = 1;
}
for(int k = 1; k <= n; k++) {
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
arr[i][j] = Math.min(arr[i][j], arr[i][k] + arr[k][j]);
}
}
}
int sum = 0;
int answer = Integer.MAX_VALUE;
int index = 0;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
sum += arr[i][j];
}
if(answer > sum) {
answer = sum;
index = i;
}
sum = 0;
}
System.out.println(index);
}
}
오늘의 회고
오늘은 어제 배운 플로이드-위셜 문제를 풀고 최소 신장 트리(MST) 이론을 학습하였습니다. 최소 신장 트리를 코드로 나타내는 것에 어려움을 많이 느꼈습니다. 주말에는 지금까지 풀었던 문제 복습과 배웠었던 알고리즘 이론들을 까먹지 않고 반복적으로 보기 쉽게 블로그에 정리하려고 합니다. 오늘은 퇴사 후 1달 정도가 되었는데 처음 알고리즘을 공부하였을 때 브론즈 5였는데 오늘은 골드 5를 찍었습니다. 앞으로 더 열심히 하겠습니다.

'알고리즘 > 알고리즘 문제풀이' 카테고리의 다른 글
| 백준) 문자열 (0) | 2022.06.21 |
|---|---|
| 백준) HashMap (0) | 2022.06.18 |
| Do it! 알고리즘 코딩 테스트 (61번) (0) | 2022.06.16 |
| Do it! 알고리즘 코딩 테스트 (57번 ~ 59번) (0) | 2022.06.15 |
| Do it! 알고리즘 코딩 테스트 (54번 ~ 56번) (0) | 2022.06.14 |